Projection coordinate system

The Projection Coordinate System (PCS), also known as the Non Earth Projection Coordinate System or simply the Plane Coordinate System, uses a coordinate system based on X and Y values to describe the position of a point on Earth.

At this point, you may ask what is the relationship between the projection coordinate system and the previous geographical coordinate system?

In fact, the geographical coordinate system is spherical coordinates, the reference plane is ellipsoidal, and the coordinate unit is longitude and latitude, while the projection coordinate system is plane coordinate system, the reference plane is horizontal, and the coordinate units are meters, kilometers, and so on.

What is projection

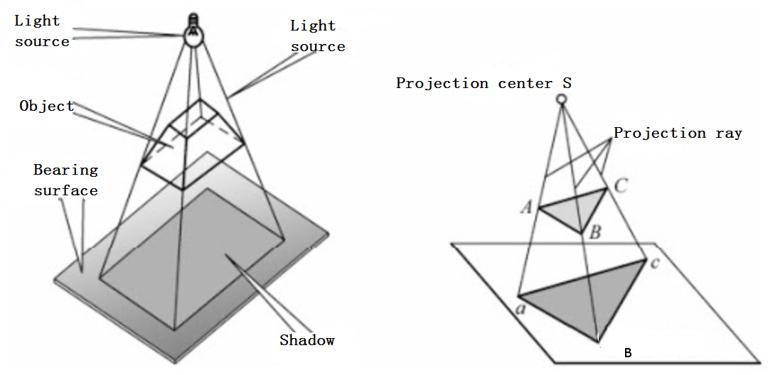
Projection refers to the use of a set of rays to project the shape of an object onto a plane called a projection. This plane is called a projection plane, and the projection we are learning is the object to be projected, which is the Earth.

The surface that can be unfolded into a plane has its own plane, and the ball can never be unfolded into a plane. Therefore, we only rely on projection to make the ball into a plane, and there are many ways of projection for the ball.

Why projection is needed

The projection is required because longitude and latitude in the geographical coordinate system do not have units, and degrees, minutes and seconds are just a decimal system. In addition, the same longitude is 1 degree, and the arc length expressed in different latitude zones is different, which brings difficulties to the area and quantitative calculation.

Traditional maps (compared with 3D platforms such as Google Earth) are presented on a two-dimensional plane, so a mapping method that can convert the three-dimensional coordinates on the earth's sphere to a two-dimensional plane is needed. This method is map projection. Therefore, map projection is a mapping method from longitude and latitude B, L, H to projection coordinates X, Y, Z.

The essence of map projection is to establish the corresponding relationship between the points on the surface of the earth's ellipsoid and the points on the map plane. The longitude and latitude coordinates under the geographic coordinate system established on the sphere are transformed into Cartesian coordinate system on the plane by a projection method.

The purpose of map projection is to establish a plane coordinate system (called projection coordinate system). Many calculations and businesses are simpler on the plane than on the surface.

For example, on a sphere, two points with the same latitude but the same longitude difference have different distances at different latitudes, which brings inconvenience to calculations. This problem does not exist on the Euclidean plane.

Many classic GIS software, such as ArcMap, have basic frameworks, including rendering, editing, and other functions developed based on 2D planes, which is consistent with our requirements for maps.

Establish a unified plane coordinate system within the allowable deformation range, and emphasize this point because the map range is also an important factor to be considered when designing map projection.

Classification of Projections

Flatten the target on the sphere to the plane, and the target will certainly be compressed or stretched. According to the nature of deformation, map projection can be simply divided into the following categories.

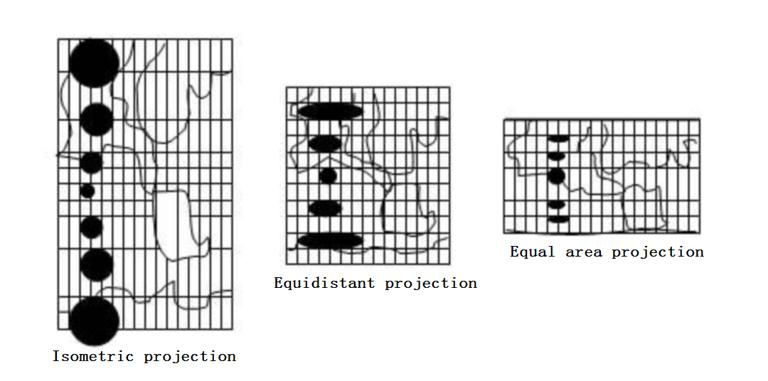
• Isometric projection: After projection, the target deforms uniformly in all directions while maintaining an overall unchanged angle

• Equidistant projection: the overall length remains unchanged after projection, and the area and angle are slightly deformed.

• Equal-area projection: assuming that there is a differential circle on the target, if the area of the circle does not change after projection, the projection is equal-area projection.

• Arbitrary projection: a projection that changes in area, angle, and length after projection.

As shown in the following figure:

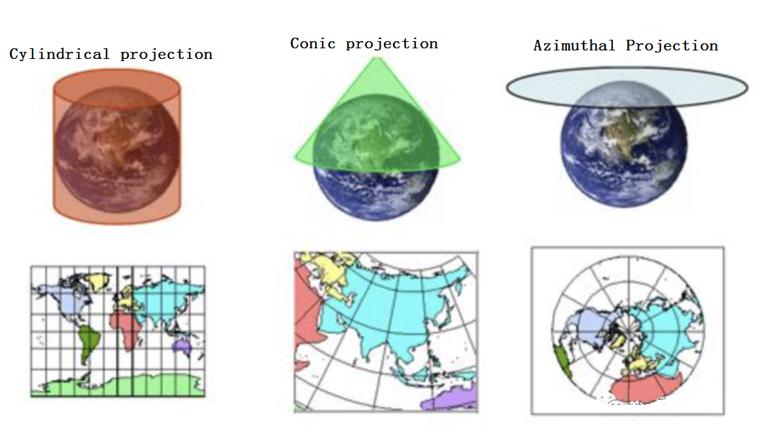
According to the projection method, it can be divided into the following categories:

• Cylinder projection: the projection surface is a cylinder
• Conical projection: The projection surface is a cone
• Azimuth projection: The projection surface is a plane

As mentioned later, the Gaussian Kruger projection is a cylindrical projection, as shown in the following figure:

According to the relative position between the main axis of the projection surface (cylinder, cone, plane) and the earth axis (short axis connecting the north and south poles), projection can be divided into the following ways:

• Positive axis projection: The central axis of the projection plane coincides with the ground axis.
• Oblique projection: The central axis of the projection plane intersects with the earth's axis diagonally.
• Horizontal projection: The central axis of the projection plane is perpendicular to the ground axis.
• Tangent projection: The projection surface is tangent to the ellipsoid.
• Cut Projection: The projection surface is cut from an ellipsoid.

Common projection methods

Mercator projection Mercator

Mercator projection, also known as Mercator projection and regular axis equiangular cylindrical projection, was created by Dutch cartographer G. Mercator in 1569.

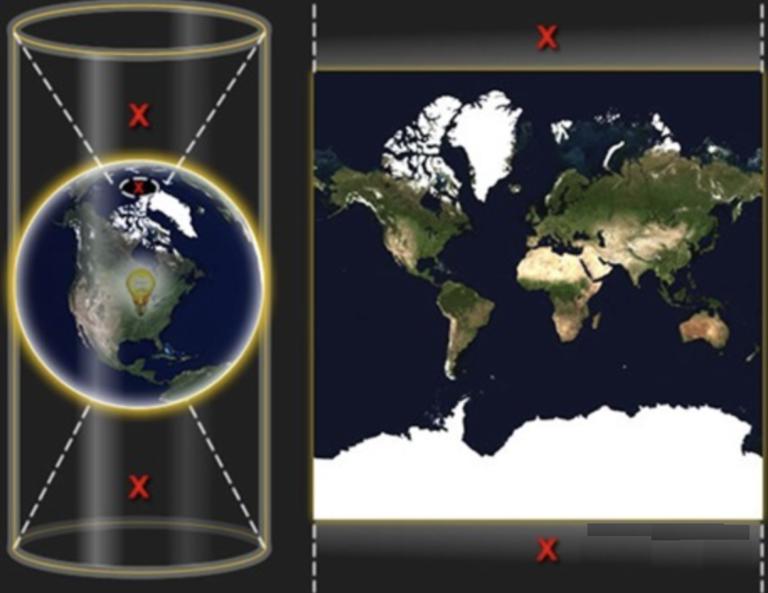
To put it simply, suppose that the earth is nested in a cylinder, the equator is tangent to the cylinder, then put a lamp in the center of the earth, project the figure on the sphere onto the cylinder, and then expand the cylinder to form a world map with Mercator projection projection, as shown below:

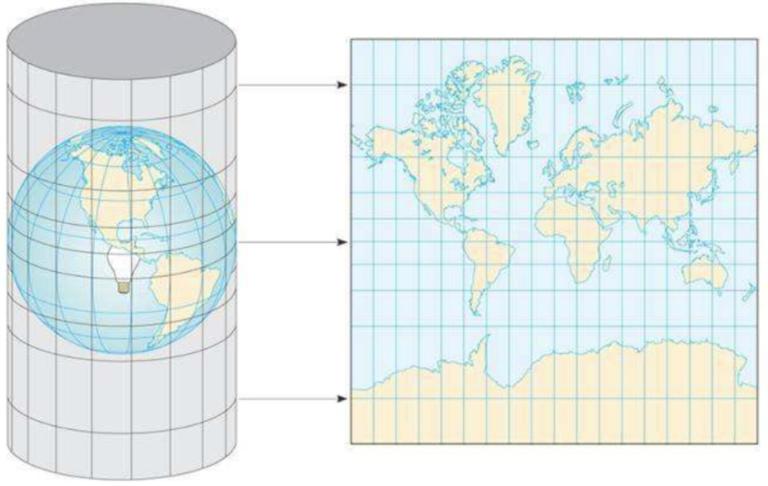
Since it can display the correct orientation between any two points, most nautical charts and route maps for navigation purposes are drawn in this way. In this projection, the linear scale remains unchanged around any point in the map, so that the angle and shape of the continental contour projection remain unchanged (that is, equiangular). However, Mercator projection will deform the area, and the proportion of poles (that is, the polar regions) will even reach infinity.

Therefore, it does not fully show the whole world. The highest latitude on the map is 85.05 degrees. In order to simplify the calculation, spherical mapping is used instead of ellipsoidal shape. Mercator projection is only used to display the map conveniently. What we need to know is that this mapping will bring 0.33% error to the Y-axis direction, as shown below:

Gauss Kruger projection

This projection was proposed by Gauss, a German mathematician, physicist and astronomer in the 1920s, and was supplemented by Kruger, a German geodetic, in 1912, so it is called Gauss Kruger projection.

You can imagine an elliptical cylinder lying horizontally on the ellipsoidal surface of the Earth (tangent to the coil), rotating around the Earth's axis, projecting the surface of the Earth onto the elliptical cylinder. After projecting onto the elliptical cylinder, it is then cut and spread along the height of the elliptical cylinder to form a plane, as shown in the following figure:

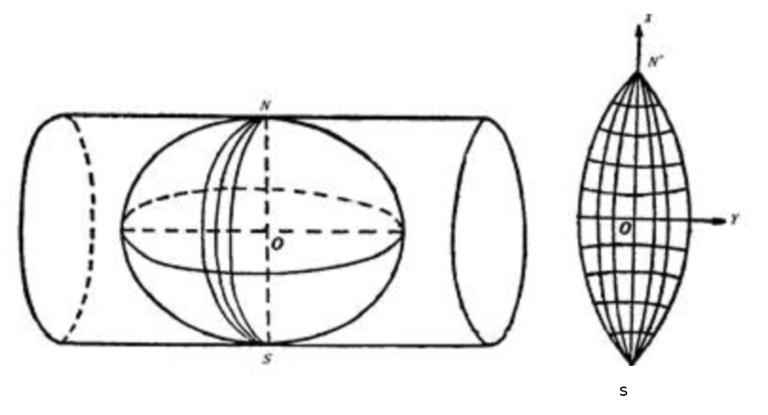
The longitude has 180 degrees east and west, and a strip is peeled off at 3 or 6 degrees to project this called a strip. By rotating the projection surface of Gaussian Kruger, the next strip's projection can be obtained to fit all parts of the world, as shown in the following figure:

The Gauss Kruger projection, also known as the equiangular crosscutting elliptic cylinder projection, is called the horizontal axis Mercator projection projection in Britain and America. The global/Universal Transverse Mercator projection (UTM) used by the United States to compile military maps and earth resource satellite images around the world is a deformation of the horizontal axis Mercator projection projection.

Universal Transverse Mercator (UTM)

The full name of UTM is Universal Transverse Mercator, which is called Universal Transverse Mercator projection in Chinese. It is very similar to the Gauss Kruger projection, except that it is not tangent to the meridian circle, but is the ellipsoid cut by the transverse normal axis of the ellipsoid (passing through the earth). The center line of the ellipsoid is located on the equatorial plane of the ellipsoid and passes through the ellipsoid body points, thus projecting the points on the ellipsoid onto the ellipsoid, as shown below:

This projection was proposed by the US Army Corps of Engineers Surveying and Mapping Bureau in the 1940s. The Clarke 1866 ellipsoid was used in the US mainland, and the WGS84 ellipsoid was used in other parts of the world. Currently, most remote sensing images are projected using the UTM projection coordinate system.

Web Mercator projection

The English name of network Mercator projection projection is PVPM (Popular Visualization Pseudo Mercator). It is not strictly Mercator projection projection, but a pseudo Mercator projection method, which was first proposed by Google Map.

Its lack of rigor lies in treating the ellipsoid representing the Earth as a normal sphere during the projection process.

It takes the entire world's equator as the standard latitude, the prime meridian as the central longitude, and the intersection of the two is the coordinate origin. It is positive when facing east to north and negative when facing west to south.

We mentioned the Mercator projection method above, so we can know that when the latitude is close to the poles, the y value tends to infinity, so these lazy engineers limit the value range of the Y axis to [- 20037508.3427892, 20037508.3427892].

Electronic maps usually display geographical coordinates in terms of longitude and latitude, while the longitude range of Mercator projection coordinates is [- 180180]. It is known that it is impossible to reach 90 ° above the latitude, and the value range is [- 85.05112877980659, 85.05112877980659].

In addition, we also need to know that the WGS84 datum is also used for WebMercator projection. Please refer to the geographical coordinate system above for datum correlation.

The commonly used PCS family of Gauss Kruger projection. In China, the geographical coordinate system is only Beijing 54, Xi'an 80, and China 2000, which can be selected according to the central longitude line as required.

The PCS family based on UTM projection is similar to the Gaussian Kruger projection coordinate system family, except that it is only based on WGS84 and can be selected according to the central meridian as needed.

China's Gaode, Baidu, Tencent maps, Google Maps, and OSM maps all use online Mercator to display flat maps. However, the geographic coordinate systems of domestic Gaode Baidu Tencent and domestic Google Maps have been encrypted. Although Tiantu uses the national 2000 geographic coordinate system, it also provides the Mercator projection method to display flat maps. ArcGIS Earth, similar to Google Earth, uses the 3857 coordinate system directly.