Concept of Map Projection #
In mathematics, the meaning of project to establish a one-to-one mapping relationship between two sets of points. Similarly, in cartography, map projection refers to the establishment of one-to-one correspondence between points on the earth’s surface and points on the projection plane. The basic problem of map projection is to use certain mathematical rules to express the longitude and latitude network on the surface of the earth on the plane. For geographic information systems, map projection must be accounted. The use of map projection guarantees the geographical connection and integrity of spatial information. In the process of establishing various geographic information systems, choosing appropriate map projection system is the first consideration. Because the surface of the ellipsoid of the earth is a surface, and the map is usually drawn on a planar drawing, the surface should first be expanded into a plane. However, the sphere is an unfoldable surface, that is, when it is directly expanded into a plane, it is impossible to avoid breaking or folding. It is obviously impractical to draw a map with such a plane with rupture or fold, so a special method must be used to unfold the surface to make it a plane without rupture or fold.
Distortion in Map Projection #
Types of Distortion #
There are numerous methods of map projection, and the graticule obtained varies in form depending on the projection method used. While projecting the spherical surface onto a plane preserves the continuity and integrity of the shapes, the resulting graticule does not fully resemble its original configuration on the sphere. This indicates that deformation occurs in the graticule after projection, and consequently, all features plotted on the map based on geographical coordinates are inevitably distorted as well. Such deformation disrupts the geometric properties, length, direction, and area of the mapped features. By comparing the graticule on a map with that on a globe, it can be observed that distortion manifests in three aspects: length, area, and angle. Length distortion and area distortion are represented by variations in scale factor and area scale, respectively. If the length distortion or area distortion is zero, then there is no distortion in length or area. Angular distortion refers to the difference between a projected angle on the map and its true corresponding angle on the Earth’s surface.
1) Length Distortion
That is, the lengths of meridians and parallels on the map are not entirely consistent with their characteristics on the globe, as they are not uniformly scaled. This indicates the presence of length distortion in the map.
On a globe, the lengths of meridians and parallels exhibit the following characteristics: First, the lengths of parallels are unequal, the equator is the longest, and the length decreases with increasing latitude, becoming zero at the poles. Second, along the same parallel, arcs with equal longitude differences have equal lengths. Third, all meridians are equal in length. The nature of length distortion varies by projection. In any given projection, length distortion not only changes from location to location but also varies with direction at the same point.
2) Area Distortion
That is, because the area of the latitude and longitude grids on the map is different from that of the geodesy, the area of the latitude and longitude grids on the map is not reduced in the same proportion, which indicates that there is an area distortion on the map.
The area of the longitude and latitude grids on the globe has the following characteristics: first, in the same latitude zone, the area of the network with the same longitude difference is equal. Second, in the same longitude zone, the higher the latitude, the smaller the network area. This is not exactly the case on maps. For example, in Figure 4-9-a, in the same latitude zone, the grid areas with equal latitude differences are equal, and these areas are not reduced in the same proportion. The higher the latitude, the larger the area ratio. In Fig. 4-9-b, the grid area with the same longitude difference varies in the same latitude zone, which indicates that the area ratio varies with the longitude. Because the area of the latitude and longitude grids on the map is different from that on the globe, the area of the latitude and longitude grids on the map is not reduced in the same proportion, which indicates that there is an area distortion on the map. Area distortion varies with projection. On the same projection, the area distortion varies with the location.
3) Angular Distortion
It means that the two angles on the map are not equal to the corresponding angles on the sphere. For example, in Figures 4-9-b and 4-9-c, only the central longitude and latitudes intersect at right angles, while the other longitudes and latitudes do not intersect at right angles, while on the globe, both longitudes and latitudes intersect at right angles, which indicates that the angle on the map is distorted. Angular distortion varies with projection. On the same projection map, the angular distortion varies with the location.
The distortion of map projection varies with the change of location, so it is difficult to say in general what distortion it has and how large the deformation is on a map. Fig. 55 Distortion of Map Projection # 
Distortion ellipse #
Distortion ellipse is a geometric figure showing distortion. As can be seen from Figure 4-9, the same size of longitude and latitude lines on the projection surface are transformed into different shapes and sizes (compared with the three grids in Figure 4-9). In practice, the distortions of each projection are different. By examining the shape and size of the distorted ellipse, which is the representation of a tiny circle on the earth’s surface (called differential circle) in the projection, the difference of the distortions in the projection can be reflected (Fig. 4-10). Fig. 56 Differential circles represent projection distortions # 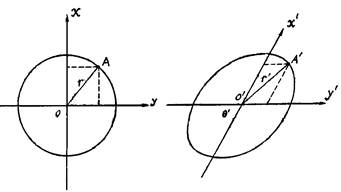
Classification of Map Projections #
There are many types of map projections. To facilitate learning and research, it is necessary to classify them. Different criteria for classification lead to different classification methods. From the perspective of map use, it is important to understand the following classifications. According to the distortion property map projection can be classified into three categories : isogonal projection, isoproduct projection and arbitrary projection. 1)Equiangular Projection It is defined that the angle projection composed of two differential lines at any point remains unchanged before and after projection, that is, the corresponding differential area before and after projection remains similar to the figure, so it can be called orthomorphic projection. The angle between any two directions of a point on the projection plane is equal to the angle between the corresponding two lines on the ellipsoid, that is, the angle distortion is zero. The length ratio of equiangular projection in any direction is equal at one point, but the length ratio is different at different locations, that is, the size of distorted ellipse is different at different locations. 2) Equal product Projection It is defined that a certain differential area remains equal before and after projection, that is, its area ratio is 1, that is, any area on the projection plane is equal to the corresponding area on the ellipsoid, that is, the area distortion is equal to zero. 3) Isometric Projection In arbitrary projections, distortions occur in length, area, and angle, making them neither conformal nor equal-area. However, one common type within this category is the equidistant projection, defined by preserving distances along a specific direction before and after projection, meaning the scale factor along that direction remains 1. This does not imply an absence of length distortion across the entire map; rather, distortion is eliminated only along that particular direction. Equidistant projections exhibit less area distortion than conformal projections and less angular distortion than equal-area projections. They are often used for maps requiring minimal distortion in both area and angle, such as general reference maps and educational maps. The length, area, and angular distortions introduced by projection are interrelated and mutually influential. Their relationship can be summarized as follows: equal-area projections cannot maintain conformality; conformal projections cannot preserve equivalence in area; arbitrary projections maintain neither conformality nor equivalence in area; equal-area projections exhibit significant shape distortion, while conformal projections show considerable area distortion. Map projection was initially based on the geometric principles of perspective, projecting the ellipsoidal surface directly onto a plane or onto developable surfaces such as cylinders or cones. Although cylindrical and conical surfaces are not flat, they can be developed into planes. This process results in geometrically derived azimuthal, cylindrical, and conical projections. With advancements in science, efforts to minimize distortion or meet specific requirements on maps led projection methods to gradually move beyond the framework of relying solely on geometric surfaces. This evolution gave rise to a series of projections constructed based on mathematical conditions. Consequently, based on the method of construction, map projections can be classified into two broad categories: geometric projections and non-geometric projections. 1) Geometric Projection Geometric projection is obtained by projecting the longitude and latitude lines mesh on the ellipsoid to the geometric surface, and then the geometric surface is expanded into a plane. According to the shape of the geometric surface, it can be further divided into the following categories (Fig. 4-11): (1.1) ** Azimuth projection**: A plane is used as a projection surface, so that the plane and the sphere are tangent or cut, and the longitude and latitude lines on the sphere are projected onto the plane. (1.2) Cylinder projection : The cylindrical surface is used as the projection surface to make the cylindrical surface tangent or cut with the sphere. The longitude and latitude lines on the sphere are projected onto the cylindrical surface, and then the cylindrical surface is expanded into a plane. (1.3) Cone projection : The conical surface is used as the projection surface, so that the conical surface and the sphere are tangent or cut, the longitude and latitude lines on the sphere are projected to the conical surface, and then the conical surface is expanded into a plane. Here, we can consider azimuthal projection as a special case of conical projection, assuming that when the apex angle of the cone is expanded to 180 degrees, the conical surface becomes a plane, and then the longitude and latitude lines on the ellipsoid of the earth are projected onto the plane. Cylindrical projection, by geometrical definition, is also a special case of conical projection. It is assumed that when the conical vertex extends to infinity, it will become a cylinder. Fig. 57 Various geometric projections # 2) Non-geometric Projection Without the help of geometric surface, the function relation between point and point between sphere and plane is determined by mathematical analytic method according to some conditions. In this kind of projection, it is generally divided into the following categories according to the shape of longitude and latitude: Pseudo-azimuth Projection : The latitude is a concentric circle, the central longitude is a straight line, and the rest of the longitude are symmetrical to the central longitude curve, and intersect at the common center of the latitude. Pseudocylindrical projection : The latitude is a parallel line, the central longitude is a straight line, the rest of the longitude are symmetrical to the central longitude curve. Pseudo-conical Projection : The latitude is a concentric arc, the central longitude is a straight line, and the other longitudes are symmetrical to the central longitude. Multi-conical projection : The latitude is an arc of the same circumference. The center of the circle is on the central meridian, the central meridian is a straight line, and the other meridians are symmetrical to the central meridian. 1) Cut Projection The plane, cylindrical or conical surface is used as projection surface to cut the projection surface from the sphere. Longitudinal and latitudinal lines on the sphere are projected onto the plane, cylindrical or conical surface, and then the projection surface is expanded into a plane. 2) Cut projection Plane, cylindrical or conical surface is used as projection surface, and the projection surface is tangent to the sphere. Longitudinal and latitudinal lines on the sphere are projected onto the plane, cylindrical or conical surface, and then the projection surface is expanded into a plane.Classification by Distortion Properties #
Classified according to the method of composition #
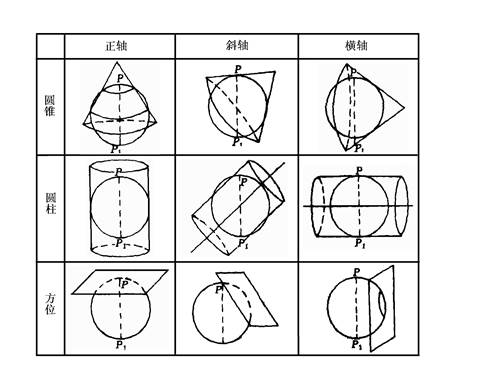
Classification by projection area cut or tangent to the earth #
Selection of Map Projection #
The appropriateness of map projection selection directly impacts the accuracy and usability of a map. The discussion of map projection selection here mainly refers to medium- and small-scale maps, excluding national basic-scale topographic maps. This is because the projection and sheet division schemes for national basic-scale topographic maps are studied and established by the national surveying and mapping authorities (currently, China adopts the Gauss-Krüger projection and its sheet division system, which will be mentioned later) and are not subject to arbitrary changes. Additionally, for large-scale maps of small areas, distortion remains minimal regardless of the projection method used.
When choosing cartographic projection, the following factors should be considered: the scope, shape and geographical location of the cartographic area, the use of maps, publishing methods and other special requirements, among which the scope, shape and geographical location of the cartographic area are the main factors.
For the world map, the main ones are the positive cylindrical, the pseudo-cylindrical and the multi-conical projections. In the world map, the Mercator projection is commonly used to draw the world route map, world traffic maps and world time zones;
Most of the world maps published in China are projected by equal difference latitudes and cones. This projection is good for representing the shape of China and the comparison with its neighbors, but the edge of projection deforms a lot.
For hemispheric maps, the horizontal axis azimuth projection is often used in the eastern and Western Hemisphere maps, the normal axis azimuth projection is often used in the southern and Northern Hemisphere maps, and the oblique axis azimuth projection is generally used in the water and land hemisphere maps.
For other medium and small range projection selection, the contour shape and geographical location should be taken into account. It is better to make the contour shape of the isomorphic line basically consistent with the contour shape of the mapping area, so as to reduce the distortion on the map. Therefore, the circular area is generally suitable for azimuthal projection, the orthogonal azimuth projection near the poles, the transverse azimuth projection in the equator-centered areas and the oblique azimuth projection in the mid-latitude areas. In the mid-latitudes extending from east to west, the orthogonal conical projection is usually used, such as China and the United States. Orthogonal cylindrical projection, such as Indonesia, should be used in areas extending East-West on both sides of the equator. Transverse cylindrical projection and multi-conical projection, such as Chile and Argentina, are commonly used in areas extending in the North-South direction.
Commonly Used Map Projections #
Projection of the World Map #
The projection of the world map mainly considers to ensure that the global deformation is not large. According to different requirements, it needs to have equiangular or iso-product properties, mainly including: iso-differential latitude multi-conical projection, tangent difference latitude multi-conical projection (1976 plan), arbitrary pseudo-cylindrical projection, orthogonal equiangular secant cylindrical projection.
Projection of a hemispheric map #
The eastern and western hemispheres have an azimuthal projection of the horizontal axis and an isometric projection of the horizontal axis. The southern and northern hemispheres have equal area azimuthal projection, equal angle azimuthal projection and equal distance azimuthal projection.
Map Projections for Continents #
Projection of Asian maps: oblique equi-area azimuth projection and Penner projection.
Projection of the European maps: oblique equal-area azimuth projection and orthogonal equal-angle conical projection.
Map projection of North America: oblique equi-area azimuthal projection and Penner projection.
Map projection of South America map: oblique equal-area azimuth projection and Thomson projection.
Projection of Australian maps: oblique equal-area azimuthal projection and orthogonal equal-angle conical projection.
Projection of a map of Latin American: oblique equi-area azimuthal projection.
Map Projections for China #
Map projection in China: oblique equal-area azimuth projection, oblique equal-angle azimuth projection, Penner projection, pseudo-azimuth projection, orthogonal equal-area secant conical projection and orthogonal equal-angle secant conical projection.
Projection of maps of provincial (regional) in China: equiangular secant conical projection, equiangular secant conical projection, equiangular cylindrical projection and Gauss-Kruger projection (broadband).
Projection of China’s large-scale map: polyhedron projection (during the period of the Northern Warlords), equiangular secant conical projection (Lambert projection) (before liberation), Gauss-Kruger projection (after liberation).